2つの円の両方に接する円
「2つの円の両方に接する円」は、赤と青の2種類ある。
赤は「片方の円に内接し、かつもう片方の円に外接する」円。中心の軌道は楕円のようだ。
青は「両方の円に内接する、または両方の円に外接する」円。中心の軌道は双曲線のようだ。
円錐を転がす動きの描画
参考:主要なオブジェクトの定義式
詳細は上記アプレットを参照ください。
円錐
Rotate(Cone( (slantHeight - radius² / slantHeight, 0, radius sqrt(slantHeight² - radius²) / slantHeight ), (0, 0, 0), radius), rotation, z軸)
円錐の一部(まだ転がっていない部分)
Surface(β x( Center + V_{sin} sin(α) + V_{cos} cos(α) ), β y( Center + V_{sin} sin(α) + V_{cos} cos(α) ), β z( Center + V_{sin} sin(α) + V_{cos} cos(α) ), α, Mod(slantHeight rotation / radius, 2π), 2π, β, 0, 1)
※ Surface( <Curve>, <Angle>, <Line>) を使った方が楽と気づき改良↓
Surface(Segment( (0, 0, 0), Contact ), 2π - Mod(slantHeight rotation / radius, 2π), Line( (0, 0, 0), Center) )
球面三角形
Twitter界隈で流行っていたので挑戦。
課題
単位球面(中心O)の表面上に、異なる3点A,B,Cをとる。
球面三角形ABCを、Surfaceコマンドで描画したい。
方針
まずは、球面三角形の辺ABを、パラメータt(0〜1)を使って表現することから。
Surfaceコマンドの癖に配慮して、AngleやRotateといったコマンド使用は避け、組み込み関数で代用していく。
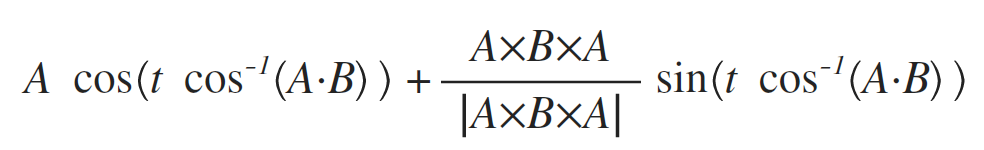
同様に、辺BCを、パラメータu(0〜1)を使って表現。
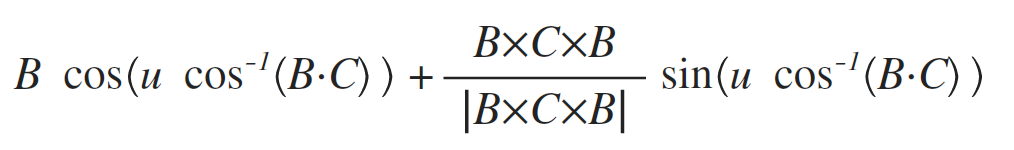
組み合わせる。
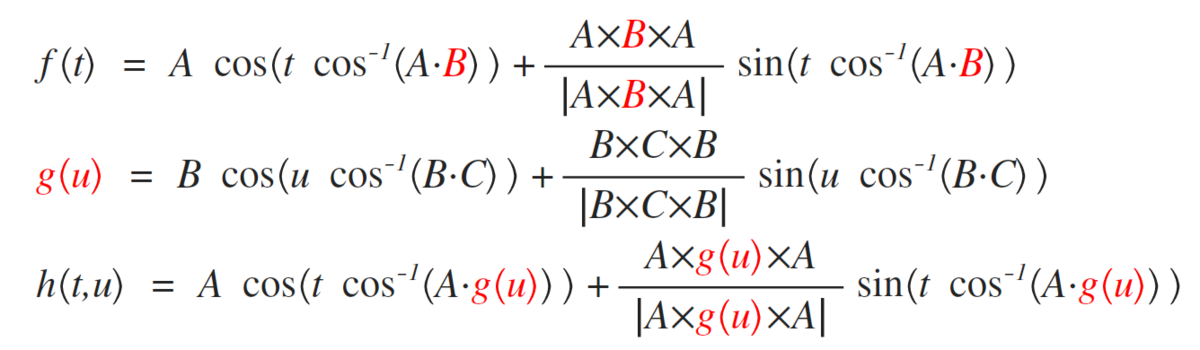
あとは、Surfaceの構文の1つである
Surface( <式>, <式>, <式>, <媒介変数1>, <開始値>, <終了値>, <媒介変数2>, <開始値>, <終了値> )
を使って終了。
上記方針で作成した場合、球面三角形ABCの、GeoGebraでの定義式はこうなる。
Surface(x((A*cos(t*acosd(A (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B))))+sin(t*acosd(A (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B))))*(A ⊗ (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B)) ⊗ A) / abs(A ⊗ (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B)) ⊗ A))),y((A*cos(t*acosd(A (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B))))+sin(t*acosd(A (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B))))*(A ⊗ (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B)) ⊗ A) / abs(A ⊗ (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B)) ⊗ A))),z((A*cos(t*acosd(A (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B))))+sin(t*acosd(A (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B))))*(A ⊗ (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B)) ⊗ A) / abs(A ⊗ (B*cos(u*acosd(B C))+sin(u*acosd(B C))*(B ⊗ C ⊗ B) / abs(B ⊗ C ⊗ B)) ⊗ A))),t,0,1,u,0,1)
……もうちょいシンプルにできないものだろうか??
なお、Surfaceを使わない方が、よほど簡単。
Sequence(CircularArc((0, 0), Point(CircularArc((0, 0), A, B), t), Point(CircularArc((0, 0), A, C), t)), t, 0, 1, 0.01)