「平面を平面で切断した片側」の描画

目次

課題

3点A(1,-1,0), B(-1,1,1), C(-1,-1,2)がある。

3点A,B,Cを通る平面p: Plane(A, B, C)を作成する。

平面q: z=1を作成する。

pをqによって切断した図形のうち、z>=1に含まれる部分を描画せよ。

サンプル

解説

方針

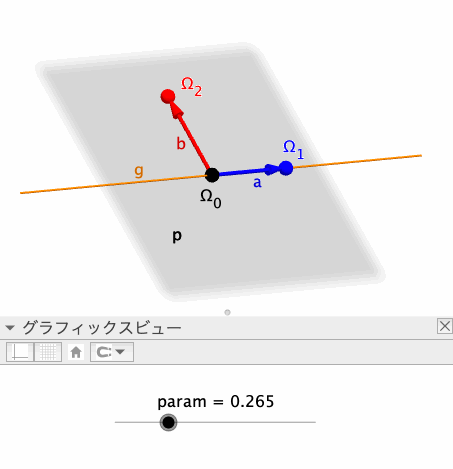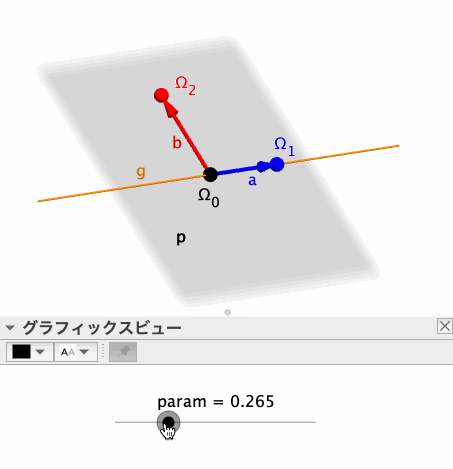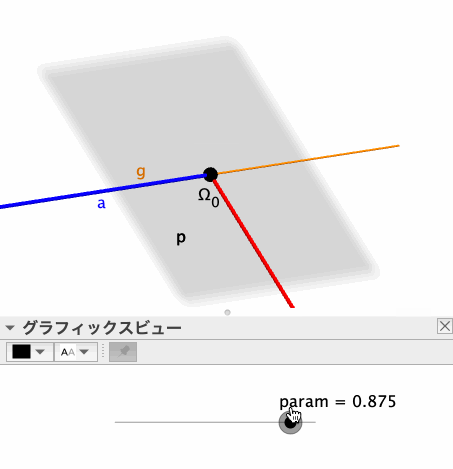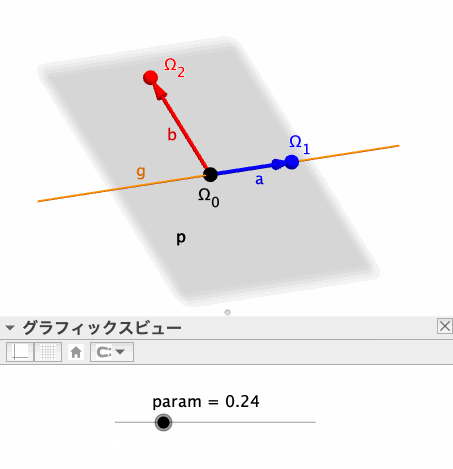
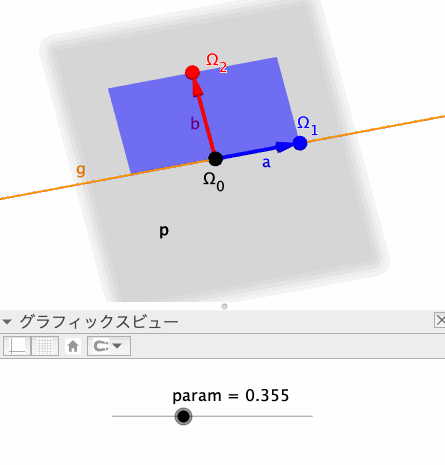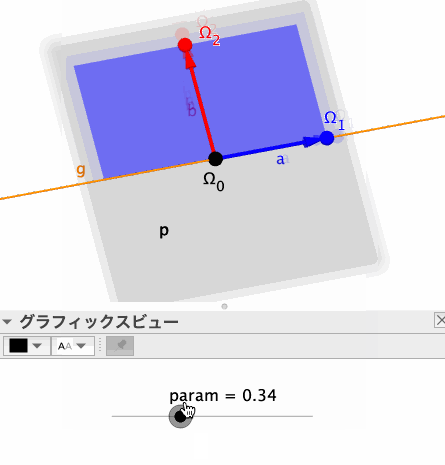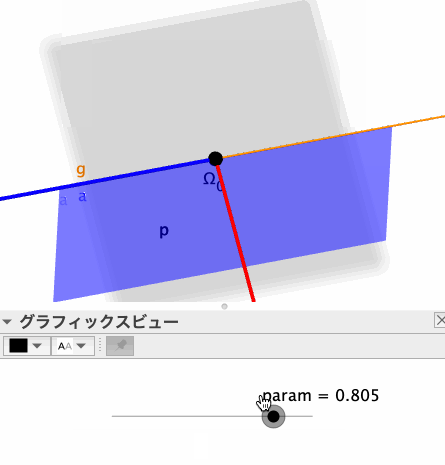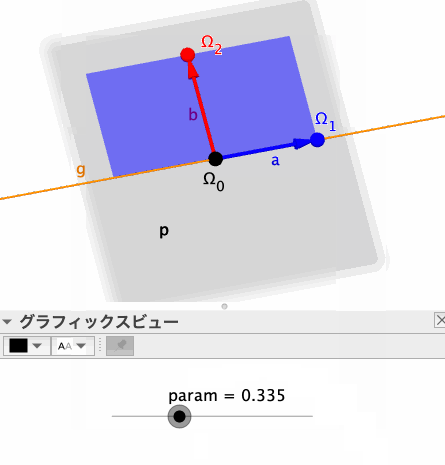
pとqの交線（上図のg、オレンジ色の線）上の2点Ω_0、Ω_1を、それぞれ始点・終点とするベクトル（上図のa）を作成する。なお、Ω_0は固定点、Ω_1は変数paramを動かすことによりg上を移動可能な点として定義する。

始点がΩ_0、終点がΩ_2（Ω_1を、Ω_0を通りpに垂直な直線を軸に90°回転移動した点）であるベクトル（上図のb）を作成する。以上の各オブジェクトの定義は、以下のとおりである。

g: IntersectionPaths(p, q)

param: Slider(0, 1, 0.001, 1, 200, false, true, true, false)

Ω_0: Point(g, 0.5)

Ω_1: Point(g, param)

Ω_2: Rotate(Ω_1, 90°, Ω_0, p)

a: Vector(Ω_0, Ω_1)

b: Vector(Ω_0, Ω_2)

ベクトルa、bと、Surfaceコマンドの構文

Surface( <式>, <式>, <式>, <媒介変数1>, <開始値>, <終了値>, <媒介変数2>, <開始値>, <終了値> )

を用いて、目的の描画を得ることを目指す。

平面pは、交線gによって2つの部分（半平面）に分けられる。このうちΩ_2を含む側を描画する。Surfaceコマンド内の媒介変数の範囲を制限することで、この図形を得る。

なお、paramが0.5より大きいか小さいかによって、Ω_2がいずれの半平面上にあるかが変わることになり、描画される半平面も変わる。目的の半平面を得られるよう、適宜paramの値を調節することにしよう。

目的の図形の描画

多変数関数pX(u,v)、pY(u,v)、pZ(u,v)を、以下の定義によって作成する。

pX: x(Ω_0) + u x(a) + v x(b)

pY: y(Ω_0) + u y(a) + v y(b)

pZ: z(Ω_0) + u z(a) + v z(b)

すると、目的の図形は

Surface(pX(u, v), pY(u, v), pZ(u, v), u, -1, 1, v, 0, 1)

によって得られる（下図の青い図形）。ベクトル先端より先は描画されないため、厳密には半平面ではないが、paramの値を調節すれば、描画範囲内を満たすことができるだろう。

オリジナルツール「HalfPlane3D」

使用例

例えば、

HalfPlane3D(y=0, x=0, 0.99)

は、下図のように、平面y=0のうち、x>=0の部分のみを描画する。

また、任意の3点A,B,Cを通る平面p: Plane(A,B,C)のうち、x>=3の部分, y>=3の部分, z>=3の部分をそれぞれ描画したいときは、

HalfPlane3D(p, x = 3, 0.001)

HalfPlane3D(p, y = 3, 0.001)

HalfPlane3D(p, z = 3, 0.001)

とすればよい。

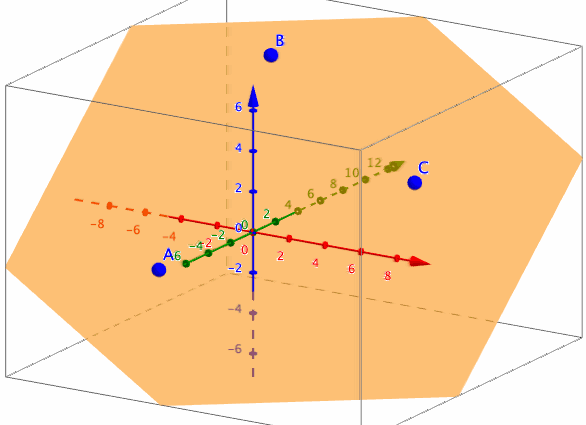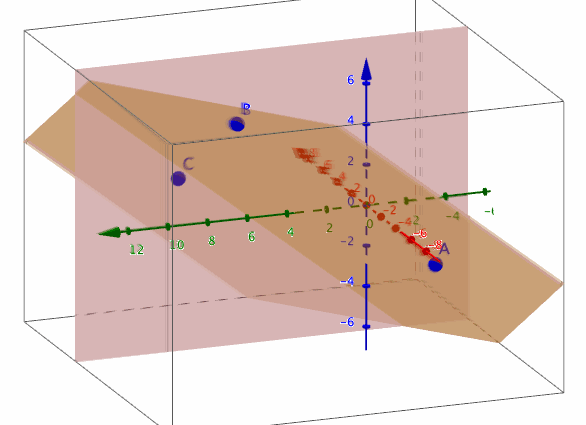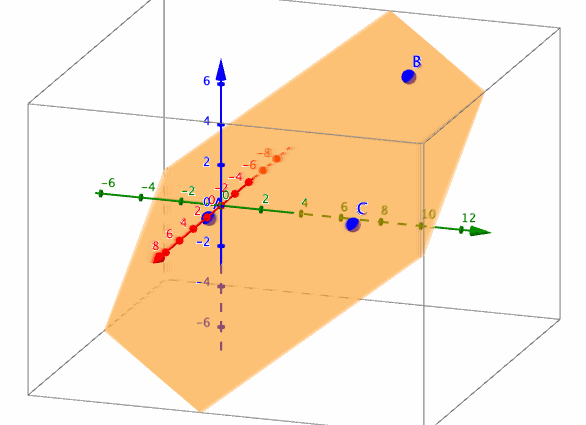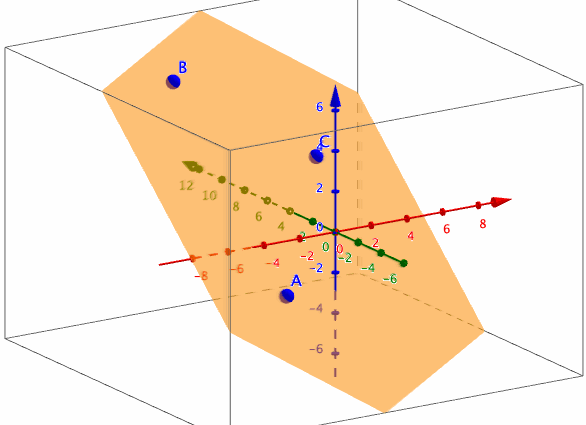
参考：ツールの定義

HalfPlane3D(<切断される平面p>, <切断する平面q>, <パラメータparam>)

≡

Surface(x(Point(IntersectionPaths(p, q), 0.5)) + u x(Vector(Point(IntersectionPaths(p, q), 0.5), Point(IntersectionPaths(p, q), param))) + v x(Vector(Point(IntersectionPaths(p, q), 0.5), Rotate(Point(IntersectionPaths(p, q), param), 90°, Point(IntersectionPaths(p, q), 0.5), p))), y(Point(IntersectionPaths(p, q), 0.5)) + u y(Vector(Point(IntersectionPaths(p, q), 0.5), Point(IntersectionPaths(p, q), param))) + v y(Vector(Point(IntersectionPaths(p, q), 0.5), Rotate(Point(IntersectionPaths(p, q), param), 90°, Point(IntersectionPaths(p, q), 0.5), p))), z(Point(IntersectionPaths(p, q), 0.5)) + u z(Vector(Point(IntersectionPaths(p, q), 0.5), Point(IntersectionPaths(p, q), param))) + v z(Vector(Point(IntersectionPaths(p, q), 0.5), Rotate(Point(IntersectionPaths(p, q), param), 90°, Point(IntersectionPaths(p, q), 0.5), p))), u, -1, 1, v, 0, 1)