f(x)=∫_0^1 |e^t-x|dtをGeoGebraで図示する

謝辞

永島 豪 先生（@Go_Nagashima）には、本稿の着想を得るきっかけを与えて頂きました。感謝申し上げます。

課題

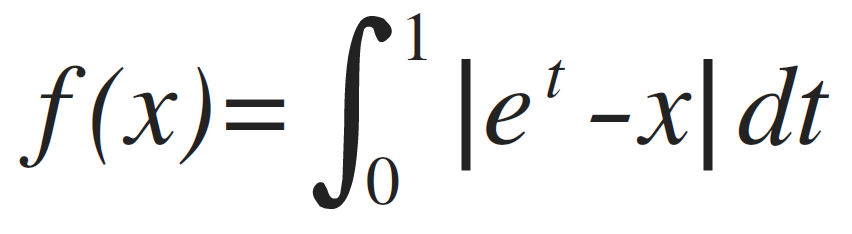
のグラフをGeoGebraで図示したい。どのようにすればよいか。

うまくいかない方法

定積分を返すコマンドである

Integral[<関数>,<開始値>,<終了値>]

は、CASモードを除き、多変数関数に対応していないようである。

CASモードで

Integral[abs(ℯ^t - x),t,0,1]

を入力すると、

sgn(x - 1) + x sgn(-ℯ + x) - ℯ sgn(-ℯ + x)

が返される。しかし、この結果は、x<=1またはx>=eの場合のみ妥当し、1<x<eには妥当しない。すなわち、 1<x<eの場合に、正しい結果（-3x+2xlog(x)+e+1）を返せていない。

解答例

現時点では、多少面倒くさいが、Locusコマンドを使った下記の方法が有用である。

①数値オブジェクトkを作成する。

②kのプロパティで、「スライダー」タブの「最小」をx(Corner[1])に、「最大」をx(Corner[2])に設定する。増分は何でも良い。

x(Corner[1])は、GeoGebraのグラフィックスビューの左下隅のx座標である。x(Corner[2])は、GeoGebraのグラフィックスビューの右下隅のx座標である。つまり、②の操作は、kのとりうる区間を、x軸のうち現在表示されている部分に揃えるという意味がある。

③kが非表示になっている場合は、表示する。

④入力バーに、

Locus[(k, Integral[abs(ℯ^x - k), 0, 1]), k]

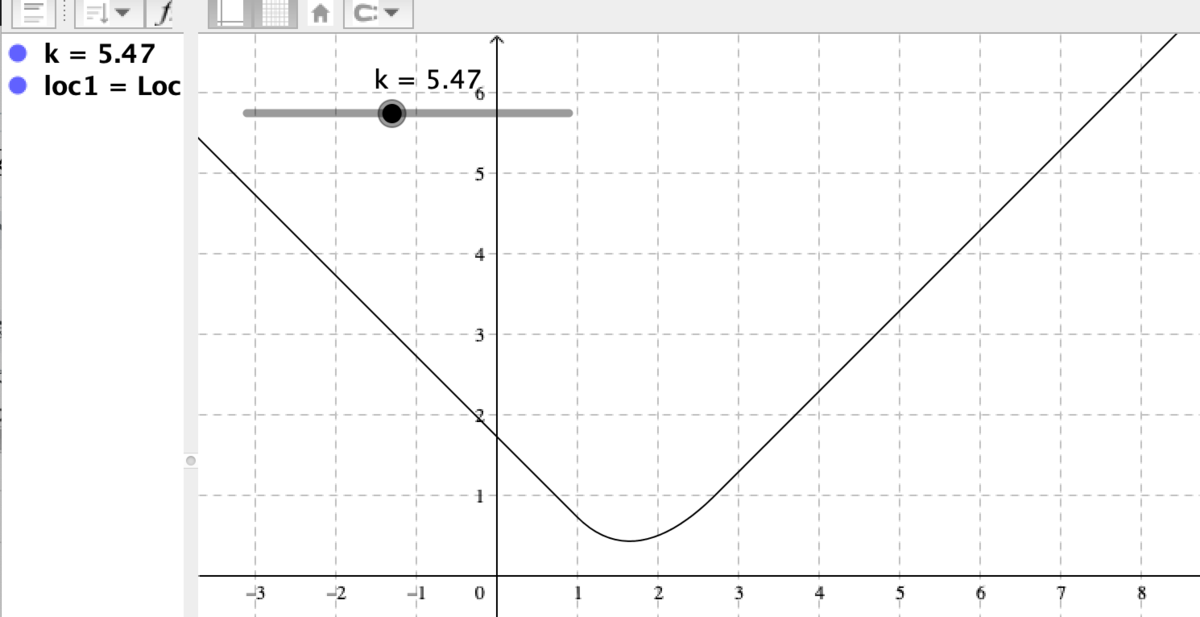
と入力する。すると、下図のように、求めるグラフが表示される。

解説

まず、定積分

を計算する。

GeoGebraでは、

Integral[abs(ℯ^x - k), 0, 1]

で計算可能である。

この定積分の値は、kによって、下図のように変化していく。

kを横軸にとって、この定積分の値の変化をグラフに描けば、求めたいグラフとなる。

このグラフを描くため、まずは、x座標がk、y座標がIntegral[abs(ℯ^x - k), 0, 1]である点オブジェクト

P=(k, Integral[abs(ℯ^x - k), 0, 1])

を作成しよう。Pは、kを動かすと、下図のような軌跡を描く（この軌跡は、Pの残像表示をONにすれば得られる）。

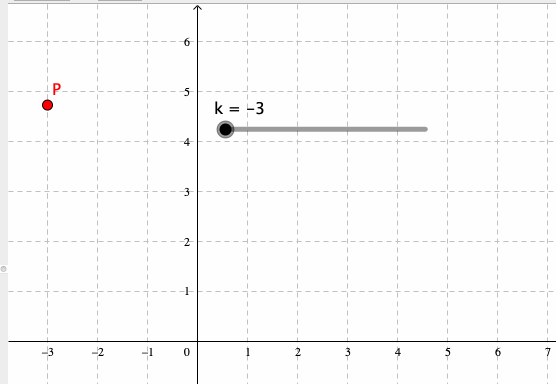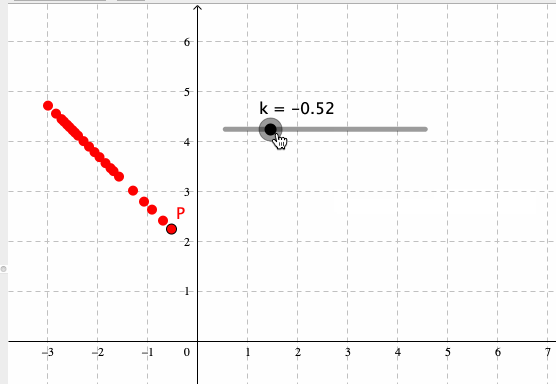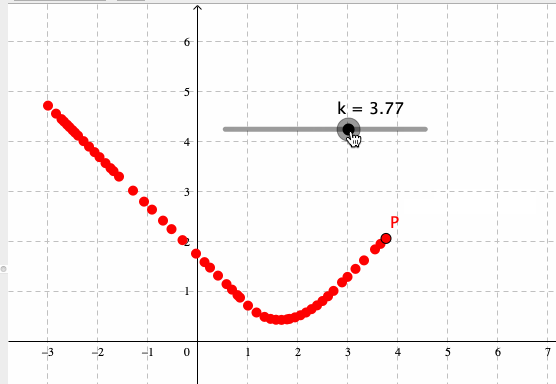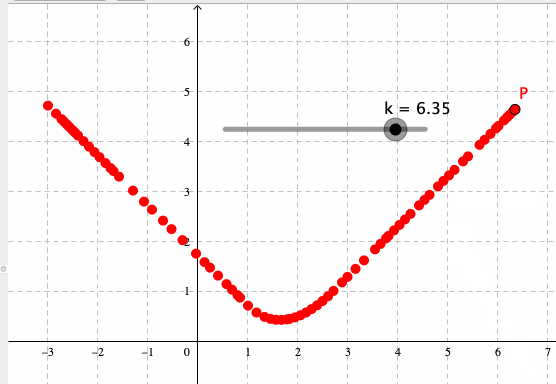
Pの軌跡を、上記のようなとびとびの残像ではなく、連続的な軌跡オブジェクトとして描くには、Locusコマンドを使えば良い。すなわち、

Locus[P,k]

と入力バーに入力すれば得られる。（なお、スライダーkを非表示にすると、軌跡がうまく描かれないので、注意されたい。）

上記「解答例」の④で述べた数式

Locus[(k, Integral[abs(ℯ^x - k), 0, 1]), k]

は、Locus[P,k]のPの部分を、Pの定義式(k, Integral[abs(ℯ^x - k), 0, 1])に置き換えたものであり、両者は同値である。

なお、描かれる軌跡は、kのスライダーの区間に限定される。上記「解答例」②で、kのとりうる区間を、x軸のうち現在表示されている部分に揃えたのは、軌跡を画面全体にわたって描くためである。

別に画面全体にわたって描く必要はなく、例えばkが-3〜3の間だけ描けばよいという場合には、kの区間を-3〜3にすればよい。