GeoGebraマジックの基本「3点スイッチャー法」のご紹介

「3点スイッチャー法」は、筆者がGeoGebraで、何か特殊なことをしようとする際に、よく使う方法です。

3点スイッチャー法とは

①自由な点オブジェクトA, B_1, B_2を作成します。

②真偽値オブジェクトswitcherを作成します。

③点B_1のOn Update ハンドラに、

SetValue[switcher,false]
SetValue[B_2,A]

と書き、点B_2のOn Update ハンドラに、

SetValue[switcher,true]
SetValue[B_1,A]

と書きます。

④点B_1のオブジェクト表示の条件を

switcher

とし、点B_2のオブジェクト表示の条件を

¬switcher

とします。

以上のような、3点（A, B_1, B_2）および真偽値（switcher）を利用した仕掛けのことを、3点スイッチャー法と呼んでいます（呼称は筆者が独自につけているだけです）。

実際のアプレットの動作の様子

3点スイッチャー法を仕掛けた場合、何が起こるのか。下記のアプレットで、実際に点を動かしてみてください。

「B_1」と書かれた赤文字が、「B_2」に変わった。もう一度ドラッグすると、赤文字が「B_1」に戻った。以下、「B_1」と「B_2」が交互に現れる。点の位置は変わらない。こういったことが分かると思います。

何が起こっているのか

点Aは、青い点であり、点B_1およびB_2は、赤い中抜きの丸で表してあります。また、上記アプレットでは、点Aの選択を許さない設定にしてあります。

「B_1」と書かれた赤文字が表示されている時は、点B_1が表示されており、点B_2は非表示になっています。このとき、点B_1をドラッグすると、点B_1は直ちに非表示になり、かわりに点B_2が、点Aの位置に現れます。

しかし、点B_1が非表示になったからといって、ドラッグ操作が解除されたわけではありません。ドラッグ操作をやめるまで、ポインタ（ないしユーザーの指）は、見えない点B_1を掴み続けているのです。

そして、いったんドラッグ操作をやめると、もう点B_1を掴み直すことはできません。点B_1が非表示になっているからです。

点B_2にも、同じことがいえます。これにより、点A上に、「ドラッグ可能な点がバトンタッチで常駐する」という状態が成立していることになります。

なお、筆者が3点スイッチャー法を実際に使う際には、点Aを非表示にして（座標を参照するためだけのオブジェクトとして利用）、2点B_1, B_2に、ともに「A」という見出しのラベルを付け、点のスタイルも揃えることで、点Aを偽装することが多いです。

利用例

3点スイッチャー法の応用範囲はかなり広いです。通常では実現できない挙動を実現できます。思いつく限りで紹介します。

点Aの移動をx軸方向だけに制限する

点B_1のOn Update ハンドラを、下記のようにします。

SetValue[switcher,false]
SetValue[A,( x(B_1),y(A) )]
SetValue[B_2,A]

点B_2のOn Update ハンドラを、下記のようにします。

SetValue[switcher,true]
SetValue[A,( x(B_2),y(A) )]
SetValue[B_1,A]

ともに2行目を新たに加えました。

そうすると、点Aの動きを、x軸方向だけに制限できます。

点Aを等積変形可能な点にする

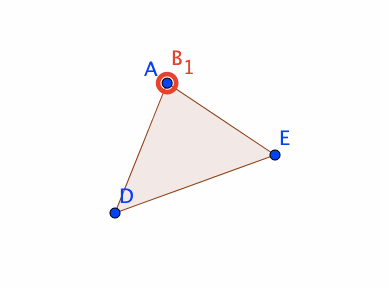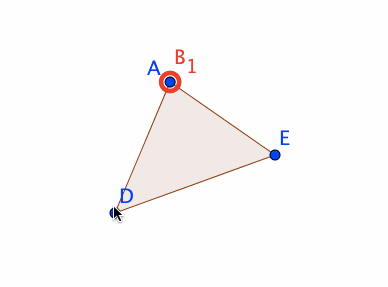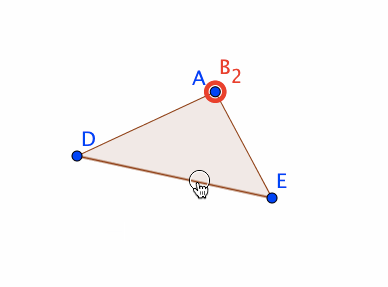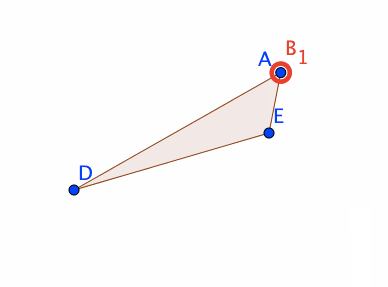
自由な点D,Eを作成し、三角形ADEを作成します。

直線f,g,hを、以下の定義で作成します。

f = Line[A, Line[D, E]]

g = PerpendicularLine[B_1, Line[D, E]]

h = PerpendicularLine[B_2, Line[D, E]]

点F,Gを、以下の定義で作成します。

F = Intersect[f, g]

G = Intersect[f, h]

点AのOn Update ハンドラを、下記のようにします。

SetValue[B_1,A]
SetValue[B_2,A]

点B_1のOn Update ハンドラを、下記のようにします。

UpdateConstruction[ ]
SetValue[switcher,false]
SetValue[A,( x(F),y(F) )]
SetValue[B_2,A]

点B_2のOn Update ハンドラを、下記のようにします。

UpdateConstruction[ ]
SetValue[switcher,true]
SetValue[A,( x(G),y(G) )]
SetValue[B_1,A]

すると、点Aの動きを、線分DEと平行な直線上に制限できます。三角形ADEをドラッグして動かした場合には、点Aは、三角形ADEの形を維持するように、三角形ADEと連動して動きます。また、点Dまたは点Eをドラッグして動かした場合には、点Aは動きません。これは、単に点Aを、線分DEと平行な直線上の点として定義した場合には実現できない挙動です。

点Aの移動を回転移動に制限する

点Aの初期位置を(2,0)とします。

点B_1のOn Update ハンドラを、下記のようにします。

SetValue[switcher,false]
SetValue[A,Dilate[B_1,2/Length[B_1]]]
SetValue[B_2,A]

点B_2のOn Update ハンドラを、下記のようにします。

SetValue[switcher,true]
SetValue[A,Dilate[B_2,2/Length[B_2]]]
SetValue[B_1,A]

すると、点Aをドラッグすると、原点から2の距離を維持しながら、原点のまわりを回転移動するようになります。

点Aの移動を回転移動に限定し、かつ、他の点を連動させる

自由な点C,Dを作成します。

点B_1のOn Update ハンドラを、下記のようにします。

SetValue[switcher,false]
SetValue[A,Dilate[B_1,2/Length[B_1]]]
SetValue[C,Rotate[C,Angle[B_2,(0,0),A]]]
SetValue[D,Rotate[D,Angle[B_2,(0,0),A]]]
SetValue[B_2,A]

点B_2のOn Update ハンドラを、下記のようにします。

SetValue[switcher,true]
SetValue[A,Dilate[B_2,2/Length[B_2]]]
SetValue[C,Rotate[C,Angle[B_1,(0,0),A]]]
SetValue[D,Rotate[D,Angle[B_1,(0,0),A]]]
SetValue[B_1,A]

すると、点Aをドラッグすると、点Aは原点のまわりを回転移動し、点C,Dも、それに伴って、同じ角度だけ回転移動します。点C,D自体は、ドラッグすることで自由に移動可能です。

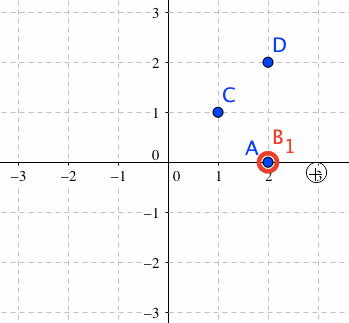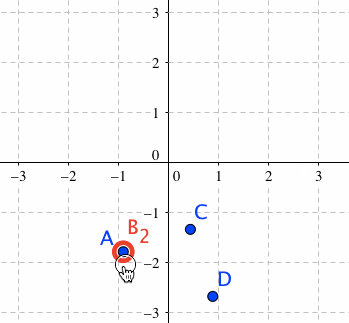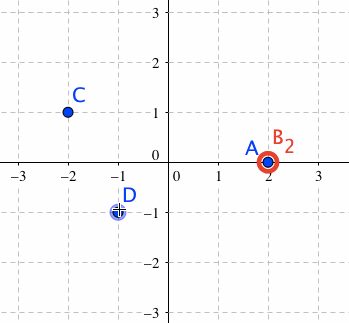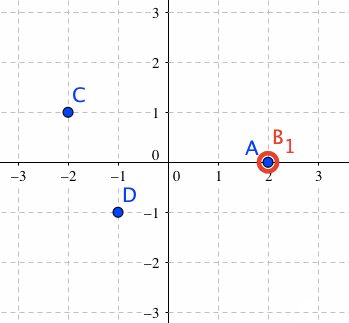
どちらのハンドラも、3,4行目で、点C,Dを動かしています。

点B_1の方のハンドラで説明すると、まず、点B_1を動かすことで、ハンドラの2行目により、点Aが回転移動をします。これによって、「回転移動前の点A」の座標に残っている点B_2との間の角の大きさ：Angle[B_2,(0,0),A]の絶対値が、0より大きい値をもちました。この角の大きさは、点B_2を「回転移動後の点A」の座標に揃える命令である、5行目が実行されることによって、0になります。よって、その直前である3,4行目を使って、当該角度分だけ、点C,Dを（原点のまわりに）回転移動させてやれば、点C,Dは、点Aに連動して回転移動するのです。

このように、ハンドラ中で「変化前の点A」と「変化後の点A」を区別することができるのは、ドラッグ可能な点が、B_1とB_2というように2つあることのお陰であり、3点スイッチャー法の特長でもあります。

その他

以前紹介した以下の記事も、3点スイッチャー法がアイデアの基本となっています。