多角形の辺に沿って点を動かす、5つの方法
課題
下図のように、任意の多角形オブジェクト(poly1)の辺に沿って、点Pを動かしたい。実現方法を考えよう。

以下では、①〜⑤の、5つの方法を紹介する。
後述するが、①②の方法では、poly1が正多角形でない場合(すなわち、辺の長さが異なる場合)には、Pを等速で動かすことができない。
辺の長さにかかわらず、Pを等速で動かしたい場合には、③④の方法が有効である。
⑤は、④の簡便法である(描画の正確性は欠けるが、④よりは作成が容易)。
- 課題
- 方法①:単にpoly1上の点をアニメーションさせる
- 方法②:スライダーと連動させる
- 方法③:スライダーを変速で動かすことで、Pの等速移動を実現する
- 方法④:スライダーを等速で動かすことで、Pの等速移動を実現する
- 方法⑤:簡便法
- 方法④の別アプローチ
方法①:単にpoly1上の点をアニメーションさせる
P = Point[poly1]
としてPを作成したうえで、Pのアニメーションを開始する。
すると、poly1の辺に沿って、Pを動かすことができる。
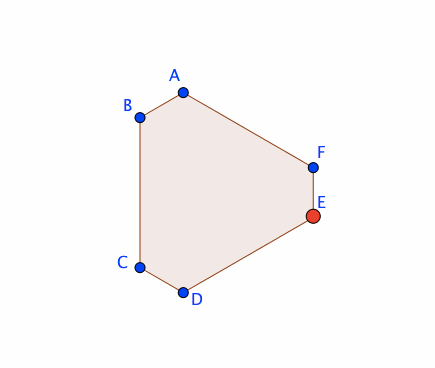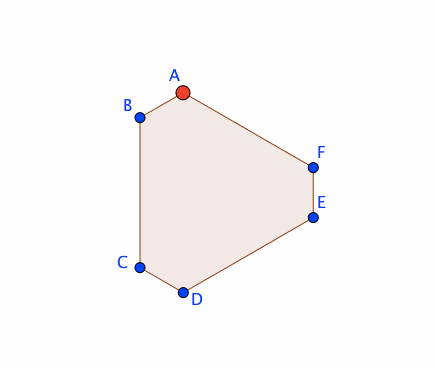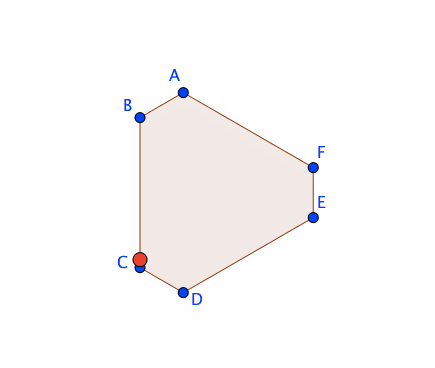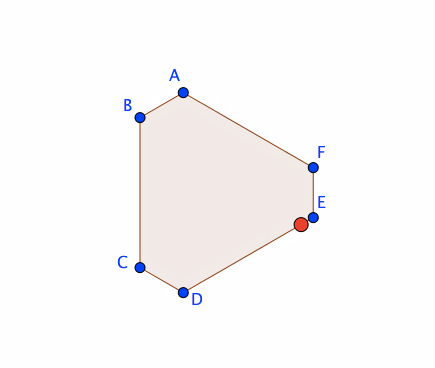
方法②:スライダーと連動させる
数値オブジェクトnを作成する。nのスライダーを、最小値-5、最大値5で作成する。
P = Point[poly1, Mod[n, 1]]
としてPを作成する。
nのアニメーションを開始することで、poly1の辺に沿って、Pを動かすことができる。
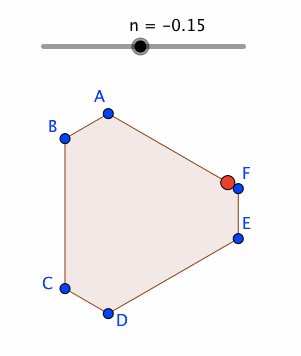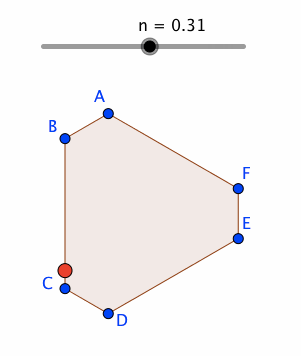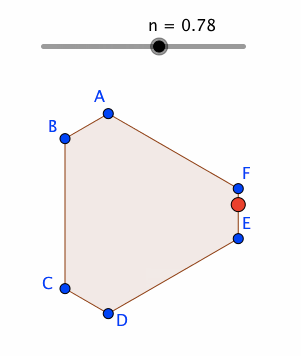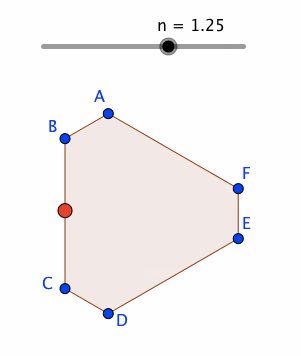
なお、パス・パラメータの意義については、下記の公式Wiki参照。
Geometric Objects - GeoGebra Manual
PathParameter Command - GeoGebra Manual
方法③:スライダーを変速で動かすことで、Pの等速移動を実現する
上記の方法①②では、Pの動く速度は、辺の長さに比例する。つまり、辺の長さに応じて、Pの速度が変わってしまう。
Pを等速で動かしたい場合は、辺の長さに応じて、nのアニメーション速度を変えるのが有効である。以下では、その具体的な方法を紹介する。
まずは、poly1の頂点のリストを作成する。
vertexList = {Vertex[poly1]}
次に、poly1の辺のリストを作成する。
sideList = Sequence[Segment[Element[vertexList, t], Element[vertexList, If[t < Length[vertexList], t + 1, 1]]], t, 1, Length[vertexList]]
点Pが現在、poly1のどの辺上にあるのかを特定し、その辺の長さを取得する。
nowLength = Sum[Zip[If[P ≟ ClosestPoint[s, P], Length[s], 0], s, sideList]]
最後に、方法②の、nのアニメーション速度を、「任意の定数 / nowLength」に設定する。例えば、
0.2 / nowLength
など。
これで、nのアニメーションを開始すると、Pが等速で動くようになる。
方法③による見本アプレット
下記URLから、方法③によって作成したアプレットにアクセスできる。
方法④:スライダーを等速で動かすことで、Pの等速移動を実現する
方法③は、nのアニメーション速度を、辺の長さに応じて変化させることで、Pの等速移動を実現した。
しかし、実用的には、nもPも、等速で動かしたい、という場合も多いだろう。そこで、これを実現する方法を、以下で紹介する。
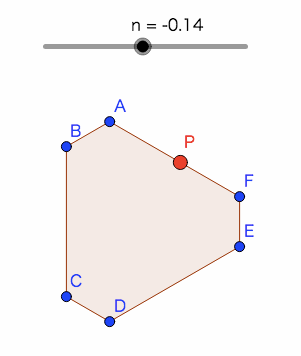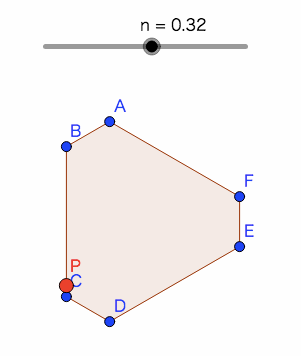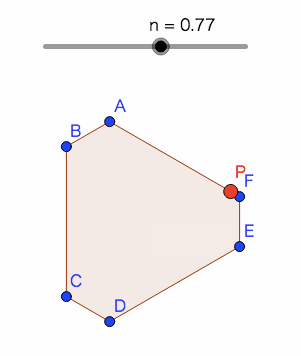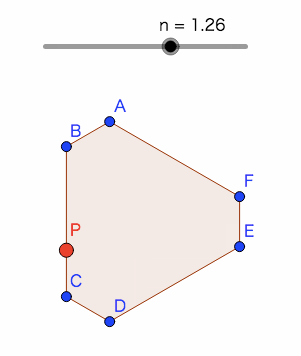
ステップ1 環境整備
poly1の頂点のリスト(vertexList)、および辺のリスト(sideList)を、以下の定義で作成する。この点は、方法③と共通である。
vertexList = {Vertex[poly1]}
sideList = Sequence[Segment[Element[vertexList, t], Element[vertexList, If[t < Length[vertexList], t + 1, 1]]], t, 1, Length[vertexList]]
ステップ2 nに対応するパス・パラメータを計算する
ここでは、nが0から1まで、等速で変化するに伴って、Pがpoly1の辺上を、等速で1周する、という挙動の実現を目指すことにする。
まずは、poly1の辺の長さの合計(totalLength)を得る。
totalLength = Sum[sideList]
次に、poly1の辺の長さを、sideListの要素の左から、順に1つずつ足していった場合の累計を、リストで取得する(sumOfSideLength)。
sumOfSideLength = Zip[Sum[sideList, IndexOf[s, sideList]], s, sideList]
例えば、下図のように、poly1 = Polygon[A,B,C]であり、sideListの要素の値が、順に3,4,5である場合(以下「仮設例」という)には、sumOfSideLengthは、{AB, AB+BC, AB+BC+CA}によって計算でき、その値は、{3,7,12}である。
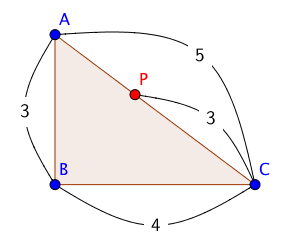
そして、sumOfSideLengthの要素のうち、Mod[n, 1] * totalLength の値(Pの移動距離を、nの1次関数として表したもの)を超えないものを抽出する(beforeAll)。
beforeAll = KeepIf[t < Mod[n, 1] totalLength, t, sumOfSideLength]
仮設例でいえば、n = 10/12のとき、すなわち、Mod[n, 1] * totalLength = 10であるとき、beforeAllの値は、{3,7}である。
beforeAllの要素数
Length[beforeAll]
は、あるnにおいて、Pがすでに通過し終わった辺の数を意味する。仮設例で説明すると、n = 10/12のとき、Pはすでに、長さ3の辺、長さ4の辺の2つを通過し終わり、長さ5の辺上を、3だけ進んだ地点に存在している。この場合、Length[beforeAll]の値は、通過し終わった辺の数「2」である。
これを利用して、Pがすでに通過し終わった辺のうち、最後に通過し終わった辺の末端(仮設例では、点C)におけるパス・パラメータを計算する(basicParam、仮設例では2/3)。
basicParam = Length[beforeAll] / Length[vertexList]
beforeAllの最後の要素を、数値オブジェクトとして得る(beforeLast)。
beforeLast = Element[Last[Join[{{0}, beforeAll}]], 1]
beforeLastの値は、Pが既に通過し終わった辺の、長さの合計を意味する。上記仮設例では、既に通過し終わった辺AB、BCの長さの和であり、その値は7である。
sumOfSideLengthの要素のうち、Mod[n, 1] * totalLength の値を超える、最小の要素の値を、数値オブジェクトとして得る(afterFirst、上記仮設例では12)。
afterFirst = Element[First[KeepIf[u ≥ Mod[n, 1] totalLength, u, sumOfSideLength]], 1]
beforeLast, n, afterFirstの3つの値の関係から、Pのパス・パラメータ(totalParam)を計算する。
extraParam = (Mod[n, 1] totalLength - beforeLast) / (afterFirst - beforeLast) / Length[vertexList]
totalParam = basicParam + extraParam
extraParamは、Pのパス・パラメータと、basicParamの差分であり、多角形の辺におけるパス・パラメータの定義に従って計算することができる。
上記仮設例では、
extraParam = { (10 - 7) / (12 - 7) } / 3 = 1/5
totalParam = 2/3 + 1/5 = 13/15
である。
ステップ3 Pを作成する
Pを、
P = Point[poly1, totalParam]
として作成すれば、Pは、nの等速変化に応じて、等速移動する。
参考:オリジナルツール「PointOnSide」
以上の作業は、非常に煩雑であるが、要はpoly1およびnを引数として、Pを定義付ける作業に他ならない。そのため、以上の作業は、poly1およびnを引数とし、Pを戻り値とする、オリジナルツールにまとめることができる。
本ツールは、多角形と数値オブジェクトを指定すれば、当該数値オブジェクトの等速変化に伴い、多角形の辺上を等速に移動するような点を返すことができる。

オリジナルツールによる見本アプレット
下記リンクより、上記オリジナルツールを使用した、見本アプレットにアクセス可能である。
多角形の辺上を等速で動く点_パラメータも等速版 – GeoGebra
方法⑤:簡便法
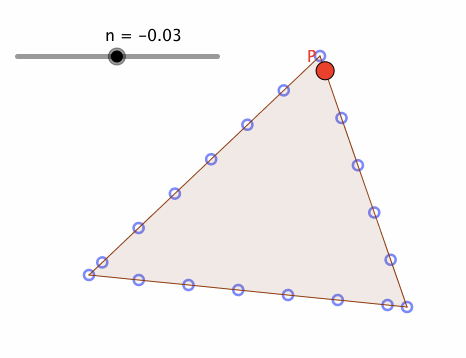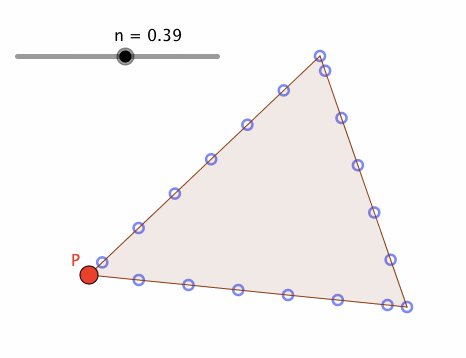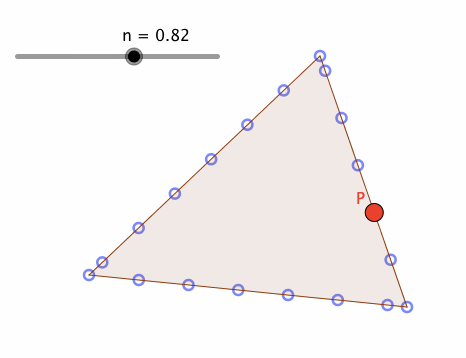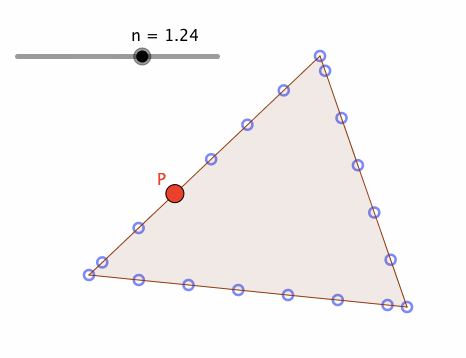
上図のように、poly1の辺上に、「できるだけ」均等に、点列(pointList)を作成し、
P = Point[pointList, Mod[n,1]]
とすれば、方法④と、ほぼ同様の挙動を実現できる。これは、方法④の簡便法と位置付けられる。
pointListの定義は、方法④におけるvertexList、および、数値オブジェクトfrequencyを所与として、
pointList = Flatten[Sequence[Sequence[Dilate[Element[vertexList, If[s + 1 ≤ Length[vertexList], s + 1, 1]], t frequency / Distance[Element[vertexList, s], Element[vertexList, If[s + 1 ≤ Length[vertexList], s + 1, 1]]], Element[vertexList, s]], t, 0, Div[Distance[Element[vertexList, s], Element[vertexList, If[s + 1 ≤ Length[vertexList], s + 1, 1]]], frequency]], s, 1, Length[vertexList]]]
である。
frequencyは、点列の間隔である。これを小さくとれば(0.01程度)、挙動の見た目は、方法④の場合と、ほぼ変わらない。
なお、下図は、frequency = 0.76の場合と、0.01の場合の挙動である。赤い点Pが、方法⑤によるものであり、黒い点P_{tool}が、方法④によるものである。
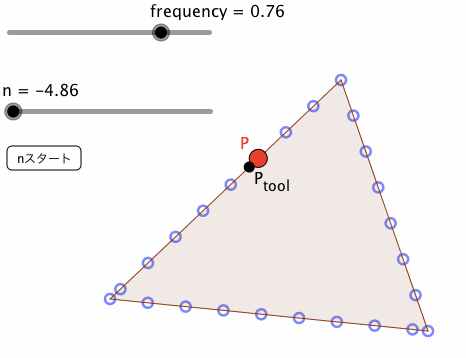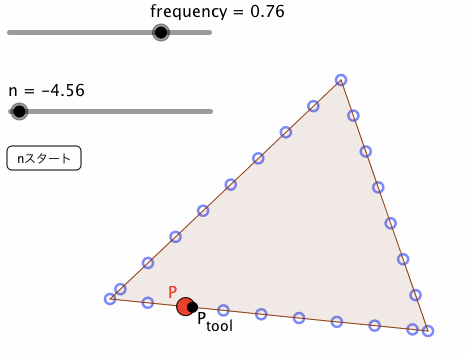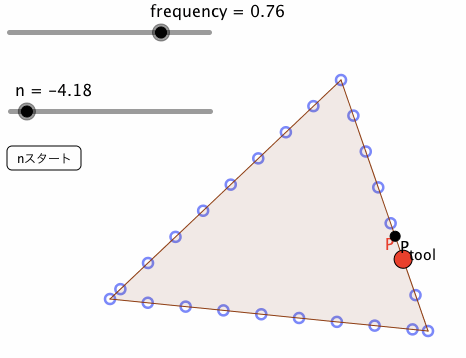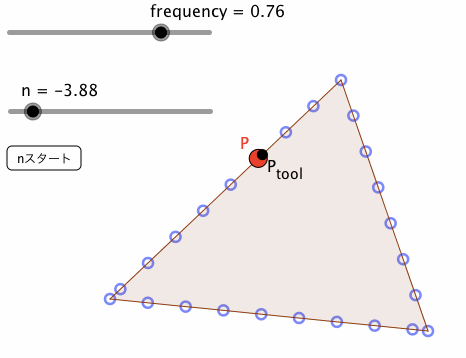
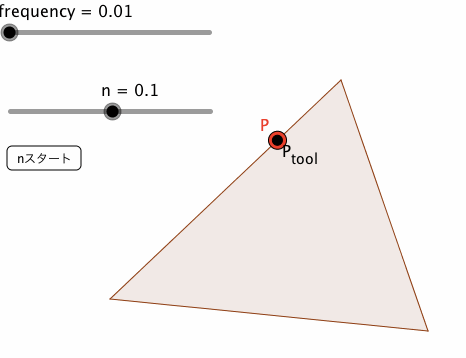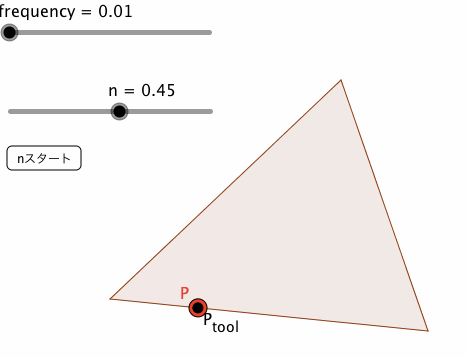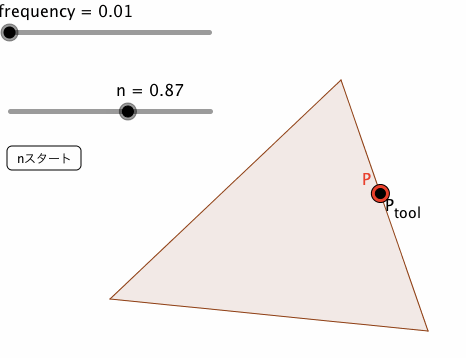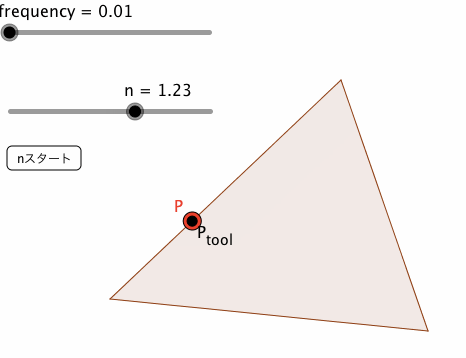
方法⑤によるアプレットには、下記URLからアクセス可能である。
多角形の辺上を等速で動く点_パラメータも等速版_簡便法 – GeoGebra
方法④の別アプローチ
方法④の別アプローチ(IfやDilateコマンドを用いたもの)によるツールも作成した。