グラフィックスビュー1におけるCornerコマンドについて
キーワード
GeoGebra, Corner, ピクセル数
目次
- はじめに
- Corner[5]と「高度な設定」におけるピクセル数との関係
- Corner[<1,2,3,4>]とアプレットの四隅との関係
- Cornerコマンドによるアプレットサイズの測定
- 補足:「プリファレンス - グラフィックスビュー」中の「次元」欄の数値とCornerコマンド
- 応用:アプレット左上隅から右にwピクセル、下にhピクセルを測定する
- オリジナルツール
はじめに
グラフィックスビューの幅および高さのピクセル数が、それぞれw, hであるとする。
このとき、
Corner[5]
は、公式wikiによれば、点(w, h)を返すコマンドであると説明される*1。
これは、グラフィックスビューの幅および高さのピクセル数を、それぞれ
x( Corner[5] )
y( Corner[5] )
によって取得することができることを意味する。
ところが、これによって取得できる値は、後述のように、アプレットのアップロード画面中「高度な設定」において指定できる、アプレットのピクセル数とは一致しない。そこで、Corner[5]の戻り値と、「高度な設定」におけるピクセル数との関係が問題となる。
また、公式wikiによれば、Corner[1],Corner[2],Corner[3],Corner[4]は、それぞれ、アプレットの左下、右下、右上、左上の隅を表す点オブジェクトを返すコマンドであると説明されている*2。
ところが、これも後述のとおり、アプレットに画像を貼付ける際、その位置の設定オプションにおいて、「隅1」をCorner[1]に設定しても、画像の左端は、アプレットの左端とは一致しない。そこで、このズレがいかなる程度のものなのかが問題となる。さらに、これを一般化すれば、Corner[1],Corner[2],Corner[3],Corner[4]が返す点と、アプレットの四隅との関係もまた、検証されるべき問題であるといえよう。
本記事では、Cornerコマンドをめぐる上記の各問題を取り扱う。なお、以下では、アプレットをアップロードする際の設定としては、メニューバー・ツールバーなど、「グラフィックスビュー1」以外のウインドウを、一切表示しない設定にすることを前提とする。
Corner[5]と「高度な設定」におけるピクセル数との関係
GeoGebraのHP上にアプレットをアップロードする際には、「高度な設定」オプションから、アプレットの幅および高さを、ピクセル数で指定できる。

そこで、これとCorner[5]の戻り値との関係をみてみよう。
モデルアプレットの作成
まず、PC版GeoGebraで、下記のようなアプレットを作成する。
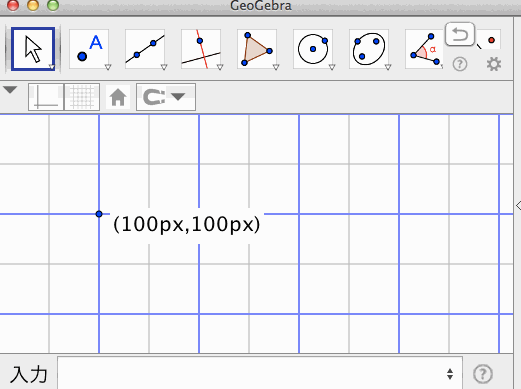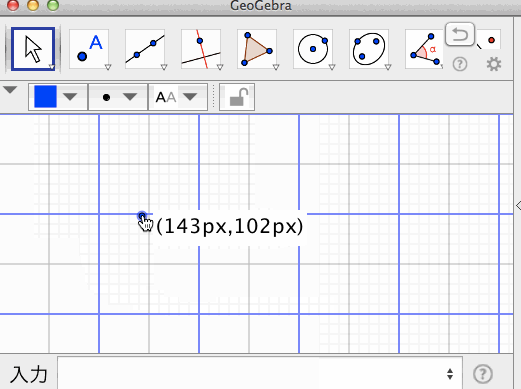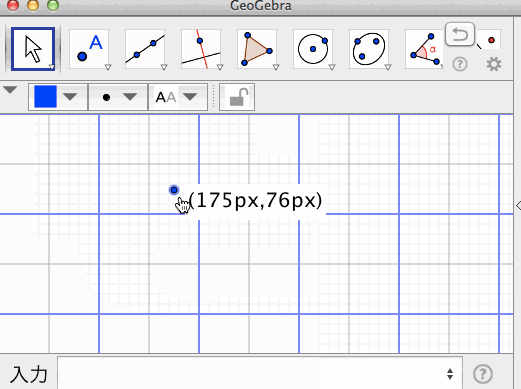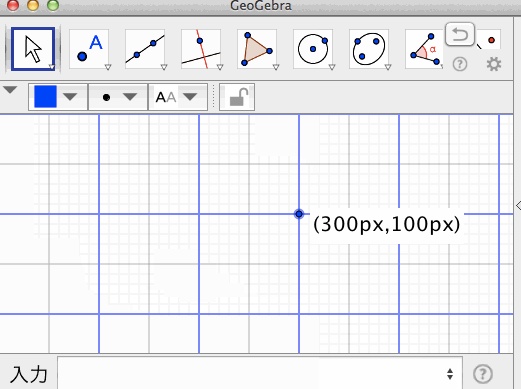
点A = Corner[5]を作成し、テキストオブジェクトを、以下の定義によって作成する。
"Corner[5]="+A
このテキストオブジェクトは、点Aの値(すなわち座標)を表す。

いま、テキストが上記のように表示されているとしよう。公式wikiの説明に従えば、現在のアプレットにおけるグラフィックスビューのサイズは、幅400ピクセル、高さ200ピクセルであるということになる。
アップロード画面におけるピクセル数
このサイズのまま、アプレットをGeoGebraのHPにアップロードしてみよう。
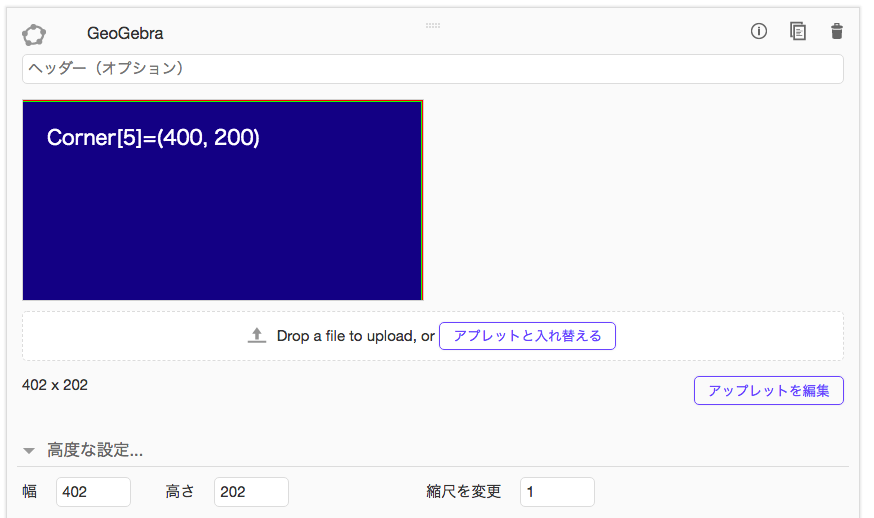
以下が、実際のアップロード画面である。
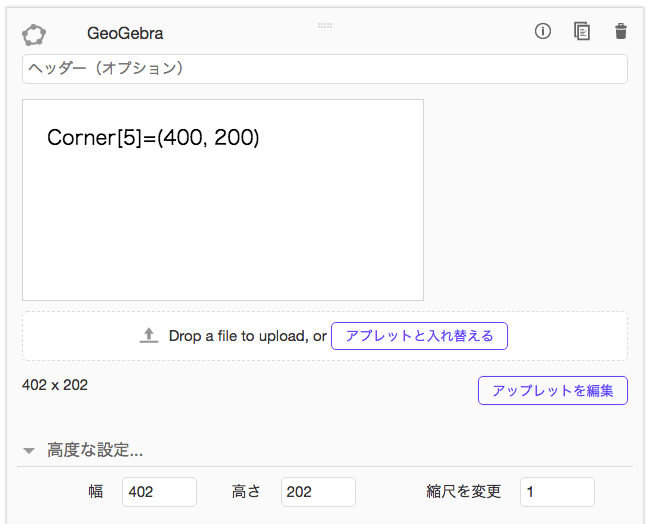
アプレット内のテキストは、400×200を示しているのに、「高度な設定」オプションにおいては、現在のアプレットのピクセル数は、402×202となっている。2ピクセルだけズレているのである。
そこで、「高度な設定」オプションにおけるピクセル数を、400×200に直してみよう。以下が、直した結果である。
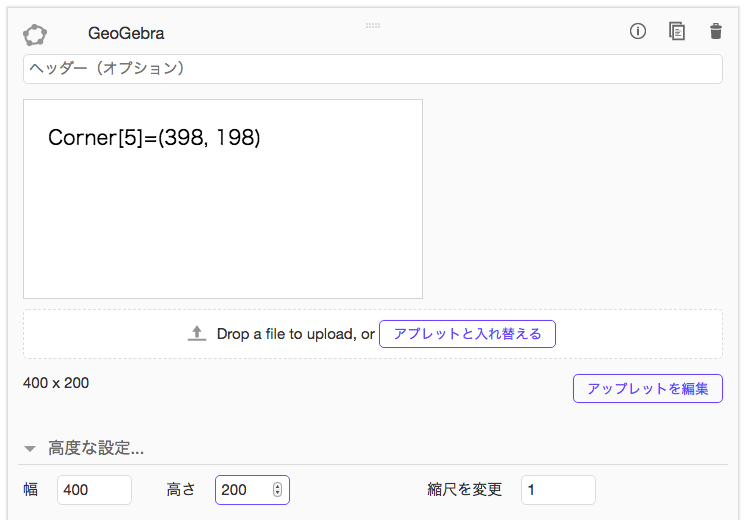
今度は、アプレット内のテキストが、398×198を示した。
このことから、Corner[5]が返すピクセル数と、「高度な設定」で指定できるピクセル数とでは、2ピクセルだけズレることが分かる。
どちらの数字が、アプレットのサイズを表す数字として正しいのだろうか。以下では、これを確かめるために、ピクセル数が分かっている画像を用いて検証する。
検証
ペイントソフトによって、400×200の画像を生成した。なお、画像の最も外側の部分を1ピクセルだけ、黄緑色に着色してある。この黄緑色の周もあわせて、400×200ピクセルである。

これを、PC版GeoGebraで、先ほどのアプレットに貼付ける。
なお、アプレットの背景画面は、「赤」に設定しておく。
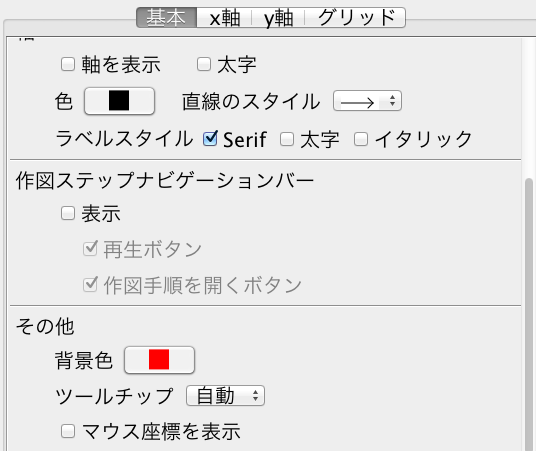
ここで、画像の貼付け位置の設定が問題となる。
「位置」オプションによる設定
まずは、画像の位置のうち「隅1」を、アプレットの左下隅であるCorner[1]に揃える方法で、画像の貼付け位置を決定してみよう。
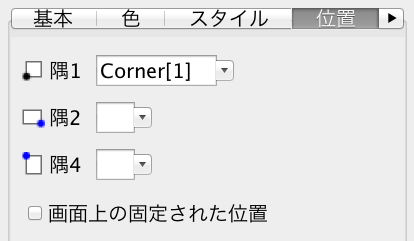
これで、GeoGebraのHPにアップロードしてみる。
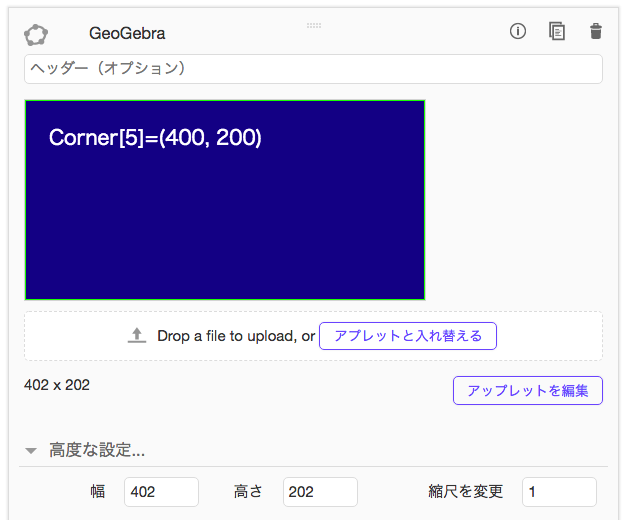
アプレット表示部分のうち、左下隅を拡大して観察してみよう。

左下には、黄緑が確認できない。これは、画像の「位置」オプションで「隅1」をCorner[1]としても、画像の左下隅と、アプレットの左下隅とが揃わないことを意味している。
なお、右上隅をみてみると、下図のように、赤と黄緑が同じ太さで観察された。

手動による設定
画像を手動でドラッグすることで、画像の左下隅とアプレットの左下隅とが揃うように、画像を配置してみよう。

上図のように、赤が消え、かつ、黄緑が残る配置は一意に決まるから、これを狙ってドラッグする。
これで、GeoGebraのHPにアップロードしてみる。
アプレットの4隅を確認してみよう。




どの隅も、赤が見えず、黄緑が見えている。つまり、400×200の画像が、過不足なくアプレットにはまっていることが分かる。
つまり、アプレットのサイズは、400×200である。
検証結果
アプレットのサイズを表す数字としては、Corner[5]コマンドの戻り値が正しい。これに対して、「高度な設定」画面におけるピクセル数は、幅・高さともに、アプレットのサイズよりも2ピクセル大きな数字を示している。アップロードの際には、この点に注意されたい。
また、このことと、画像の位置のうち「隅1」をCorner[1]にした場合に、右上隅において赤と黄緑が同じ太さで観察されたこととを併せ考えると、画像の位置のうち「隅1」をCorner[1]にした場合には、画像の左下隅は、アプレットの左下隅から、左に1ピクセル、下に1ピクセルだけズレることが分かる。
以下では、Corner[1],Corner[2],Corner[3],Corner[4]が返す点と、アプレットの四隅との関係について、さらに調査してみよう。
Corner[<1,2,3,4>]とアプレットの四隅との関係
サイズ1の点オブジェクトの表示態様
通常表示
任意の点をとり、色を青、サイズを1に設定した場合、その点の表示態様は、下図のとおりである。

点の部分を拡大すると、下図のとおり、PC版GeoGebra(バージョン5.0.321.0-3D。以下同じ)では、ピクセル数4×4の正方形内にぴったり収まるように描画されることがわかる。

web版GeoGebra(バージョン6.0.461.0-w。以下同じ) では、下図のとおりである。

PC版と同様に、ピクセル数4×4の正方形内にぴったり収まるように描画されているが、四隅が描画されていない点は、PC版と若干異なる点であるといえよう。
強調表示
点を選択して強調表示した場合には、PC版GeoGebraでは、下図のとおり、ピクセル数6×6の正方形内にぴったり収まるように描画される。

web版では、下図のとおり、ピクセル数8×8の正方形内にぴったり収まるように描画される。

小括
ここまでで、サイズ1のある点が、一定のピクセル数の正方形にぴったり収まるように描画されることが確認できた。
そして、点の位置は、この正方形の中心(描画の中央)であることが推察される。
以下では、上記のことが、サイズ1のすべての点について当てはまるとの仮定のもとで、調査を進めることとする。
Corner[<1,2,3,4>]の描画態様
Corner[1]を作成し、その色を青、サイズを1にした場合の描画態様を確認してみよう。
PC版GeoGebra

画像右上の白い部分が、グラフィックスビューであり、画像中央に見える暗いグレーの縦棒・横棒が、ウインドウの境界線である。グラフィックスビューの左下隅に、薄いグレーの1ピクセルが描画されていることがわかる。
作成したCorner[1]を選択して、強調表示した場合は、下図のとおりである。

グラフィックスビューの左下隅に、青または薄い青で、3ピクセル分が描画されていることが分かる。
web版GeoGebra
web版でも同様の操作を行い、確認してみよう。

画像右上の白い部分が、グラフィックスビューであり、画像中央に見える暗いグレーの縦棒・横棒が、ウインドウの境界線である。グラフィックスビューの左下隅には、何も描画されていない。
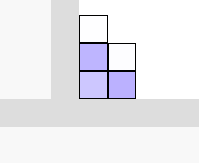
強調表示した場合は、下図のとおりである。

薄くて見えにくい部分もあるが、描画されている部分を格子で囲むと、下図のように、5ピクセル分が描画されていることが分かる。
考察
以上の結果をみると、Corner[1]をサイズ1で作成した場合には、その一部分のみがグラフィックスビューに描画されていることが推察される。
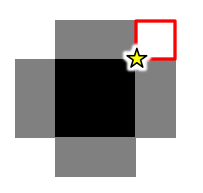
そこで、描画されている部分を赤枠で強調すると、以下のようになろう(順に通常表示、強調表示)。そして、グラフィックスビューの左下隅は、その赤枠の図形の左下隅(下図において黄色い★印を付した場所)ということになる。
PC版GeoGebra

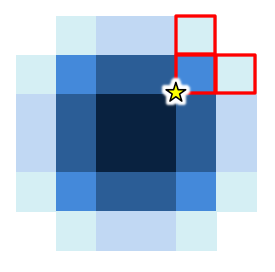
web版GeoGebra
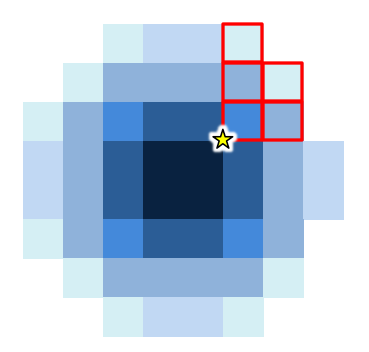
ところで、点Corner[1]自体の位置は、前述のとおり、描画の中央である。
しかし、PC版でもweb版でも、グラフィックスビューの左下隅(★印の場所)は、描画の中央から右へ1ピクセル、上へ1ピクセルだけずれている。
このことから、Corner[1]は、グラフィックスビューの左下隅から、左へ1ピクセル、下へ1ピクセル移動した場所を示す点を作成するコマンドであることが分かる。
換言すれば、Corner[1]の位置は、グラフィックスビューの左下隅よりも、左下に1ピクセルだけズレているということだ。
なお、Corner[2],Corner[3],Corner[4]についても、同様の結果が得られた。
Cornerコマンドによるアプレットサイズの測定
これまでの調査結果を踏まえて、Cornerコマンドによってアプレットのサイズを測定する方法をまとめると、以下のようになる。
ピクセル数による測定
幅、高さの順に、
x( Corner[5] )
y( Corner[5] )
座標による測定
x( Corner[2] ) - x( Corner[1] ) *3は、アプレットの幅に2ピクセルを加えた分の長さを、座標で測定した値であるといえる。
なぜならば、Corner[1]やCorner[2]は、アプレットの隅そのものから、それぞれ1ピクセル外側の点を返すからである*4。
したがって、
x( Corner[5] ) + 2:ピクセル表示
と、
x( Corner[2] ) - x( Corner[1] ):座標表示
とが対応する。
そのため、アプレットのサイズを座標で測定する計算式は、
幅
x( Corner[5] ) ( x( Corner[2] ) - x( Corner[1] ) ) / ( x( Corner[5] ) + 2 )
高さ
y( Corner[5] ) ( y( Corner[4] ) - y( Corner[1] ) ) / ( y( Corner[5] ) + 2 )
となる。
補足:「プリファレンス - グラフィックスビュー」中の「次元」欄の数値とCornerコマンド
「プリファレンス - グラフィックスビュー」ウインドウでは、アプレットが表示している座標平面の範囲を確認ないし指定できる。
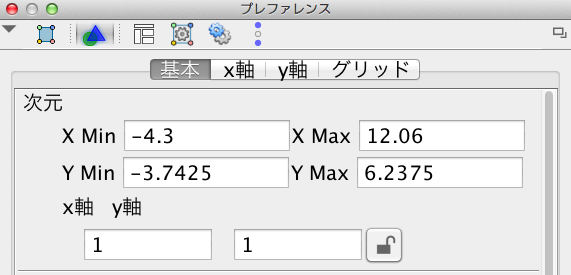
ここで、「X Min」は、アプレットの左端のx座標である。換言すれば、x( Corner[1] )を、x軸方向に1ピクセル移動した点のx座標である。
1ピクセルをx座標ベースで測定したときの値は、
( x( Corner[2] ) - x( Corner[1] ) ) / ( x( Corner[5] ) + 2 )
であるから、「X Min」の値は、
x( Corner[1] ) + ( x( Corner[2] ) - x( Corner[1] ) ) / ( x( Corner[5] ) + 2 )
と一致する。
同様に、残りの値の計算式をまとめると、以下のようになる。
X Max
x( Corner[2] ) - ( x( Corner[2] ) - x( Corner[1] ) ) / ( x( Corner[5] ) + 2 )
Y Min
y( Corner[1] ) + ( y( Corner[4] ) - y( Corner[1] ) ) / ( y( Corner[5] ) + 2 )
Y Max
y( Corner[4] ) - ( y( Corner[4] ) - y( Corner[1] ) ) / ( y( Corner[5] ) + 2 )
なお、x座標の場合とy座標の場合とでは、第2項を、それぞれ
( x( Corner[2] ) - x( Corner[1] ) ) / ( x( Corner[5] ) + 2 )
と
( y( Corner[4] ) - y( Corner[1] ) ) / ( y( Corner[5] ) + 2 )
とに使い分けている。
これは、例えば下図のように、x座標1の長さと、y座標1の長さが異なる場合には、1ピクセルをx座標ベースで測定したときの値と、y座標ベースで測定したときの値が一致しないから、こうした場合に備えて使い分けているのである。
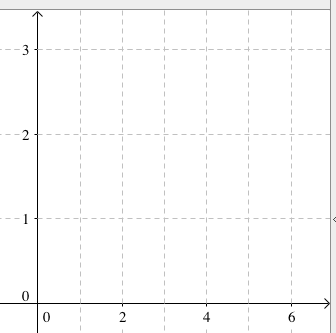
応用:アプレット左上隅から右にwピクセル、下にhピクセルを測定する
アプレットの左上隅から、右にwピクセル、下にhピクセル進んだ位置にある点を作成するには、どうすれば良いだろうか。
求めたい位置は、Corner[4]から出発した場合には、そこから右に(w+1)ピクセル、下に(h+1)ピクセルだけ進んだ位置である。
したがって、(w+1)ピクセルをx座標ベースの値に変換し、(h+1)ピクセルをy座標ベースの値に変換し、それぞれの値を、Corner[4]のx座標、y座標に加減すればよい。
結論
アプレットの左上隅から、右にwピクセル、下にhピクセル進んだ位置にある点は、
Corner[4] + ( (w + 1) ( x(Corner[2]) - x(Corner[1]) ) / ( x(Corner[5]) + 2 ), -(h + 1) ( y(Corner[4]) - y(Corner[1]) ) / ( y(Corner[5]) + 2 ) )
によって作成することができる。
確認
実際のアプレットで確認してみよう。
前掲の400×200の画像を、その左上隅とアプレットの左上隅とが一致するように配置する。
そして、w=400, h=200として、上記結論の数式を実行して、点を得る。
作成された点を拡大したのが、下図である。
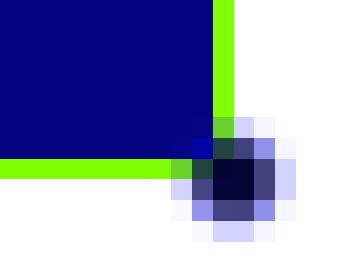
点の描画(PC版、強調表示)の中央と、画像の右下隅とが、ぴったり一致していることが分かる。このことから、この点は、アプレットの左上隅から、右に400ピクセル、下に200ピクセル進んだ位置にあることが確認できた。以下、この点をQとする。
ピクセル数で表された領域の可視化
点Qを用いて、アプレットの左上隅から右に400ピクセルまで、下に200ピクセルまでの領域を可視化してみよう。
アプレットの(ちょうど)左上隅の点は、
Corner[4] + ( ( x(Corner[2]) - x(Corner[1]) ) / ( x(Corner[5]) + 2 ), - ( y(Corner[4]) - y(Corner[1]) ) / ( y(Corner[5]) + 2 ) )
である。この点をPとする。
Polygon[ P, ( x(P), y(Q) ), Q, ( x(Q), y(P) ) ]
を作成し、直線の太さを0にする。
この長方形は、アプレットの左上隅から右に400ピクセルまで、下に200ピクセルまでの領域を示す(各自確認されたい)。
オリジナルツール
今回の検討の副産物として、いくつかのオリジナルツールができたので、以下に配布する。
ピクセル領域:Pixel[ <数値>, <数値> ]
幅と高さのピクセル数を指定すると、その大きさの領域を可視化する。
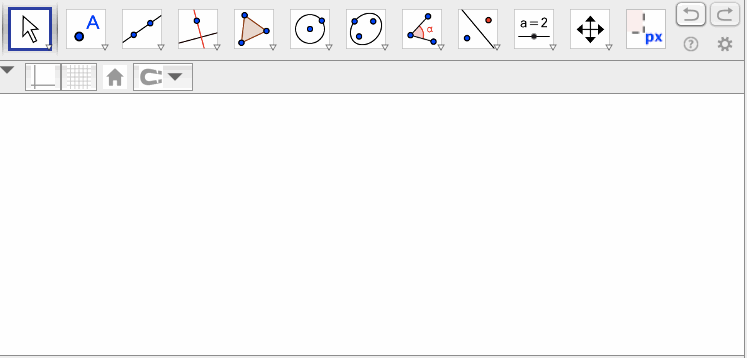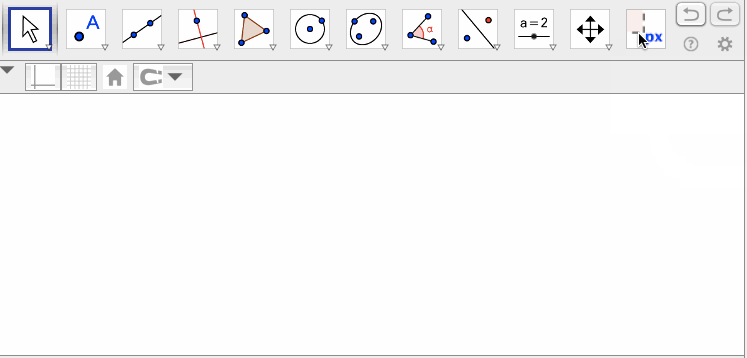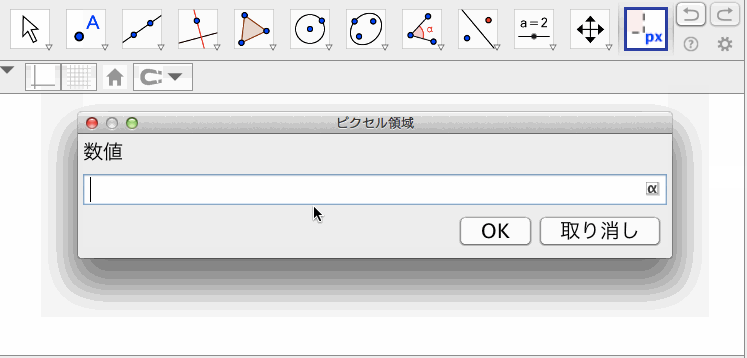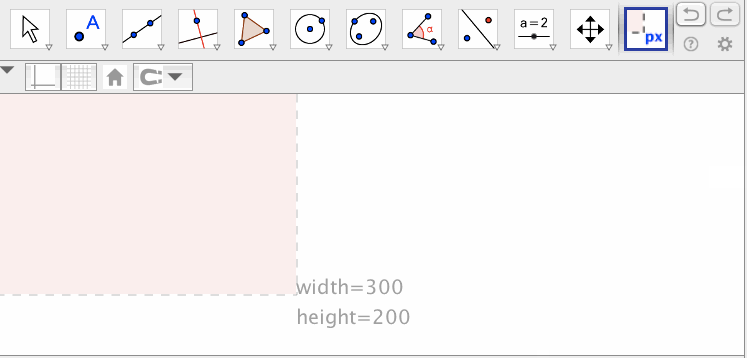
薄い赤の領域が、指定したピクセル数の領域である。灰色の点線は、その領域に含まれない。
アップロード時には、それぞれのピクセル数に2を足した値を、「高度な設定」にて指定する必要がある点は、前述のとおりである。
四隅上の点:InternalCorner[ <数値> ]
InternalCorner Tool - GeoGebra
数値は、1,2,3,4のいずれかをとる。順に、グラフィックスビューの左下、右下、右上、左上の隅の点を返す。
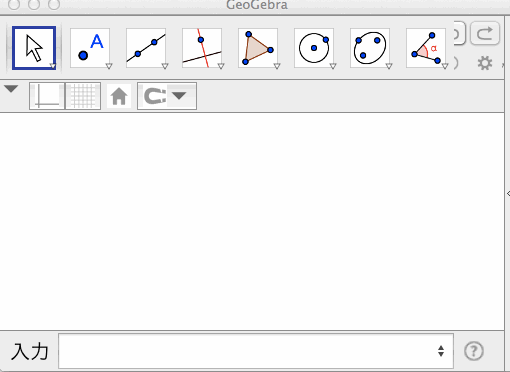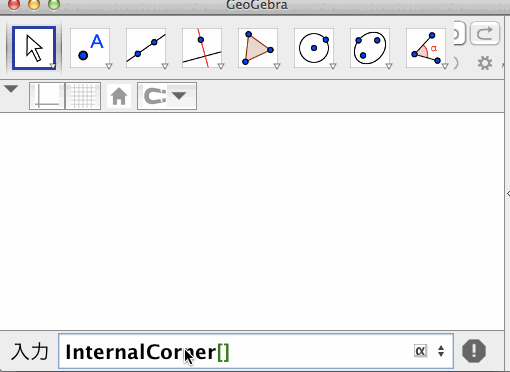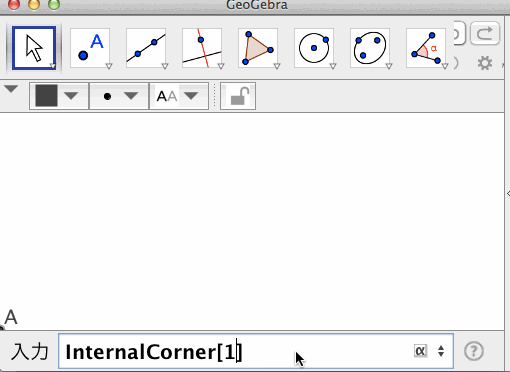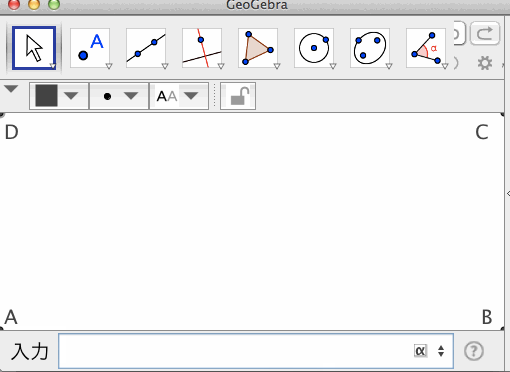
前述のとおり、Corner[ <1,2,3,4> ]は、グラフィックスビューの隅ぴったりの点ではなく、隅から1ピクセル外側の点である。これに対して、本オリジナルツールは、隅ぴったりの点を返せるツールである。
ピクセル座標:PixelCoords[ <点> ]
指定した点が、グラフィックスビューの左上隅から、右にwピクセル、下にhピクセルの位置にあるとき、点 (w, h) を返すオリジナルツールである。
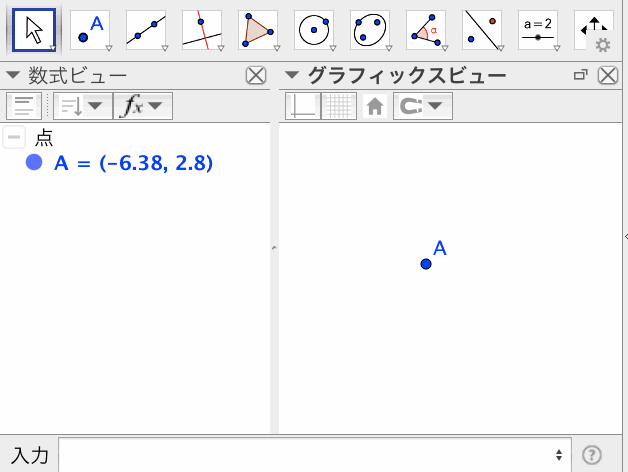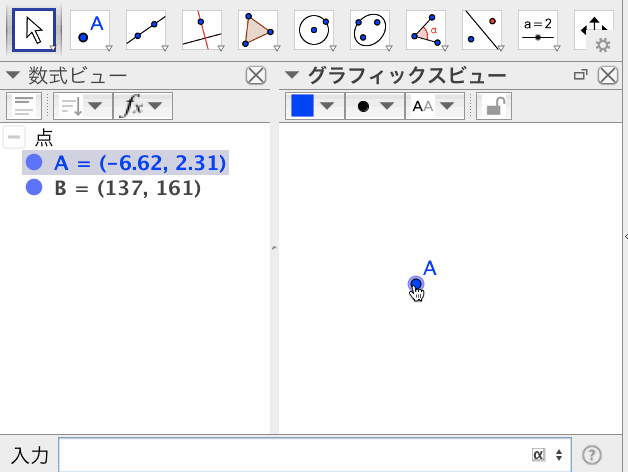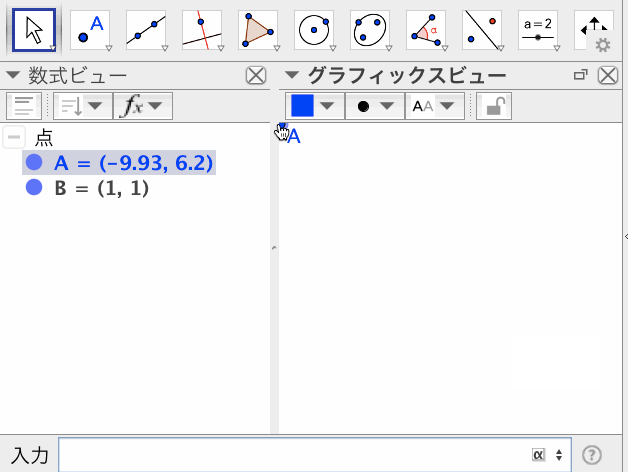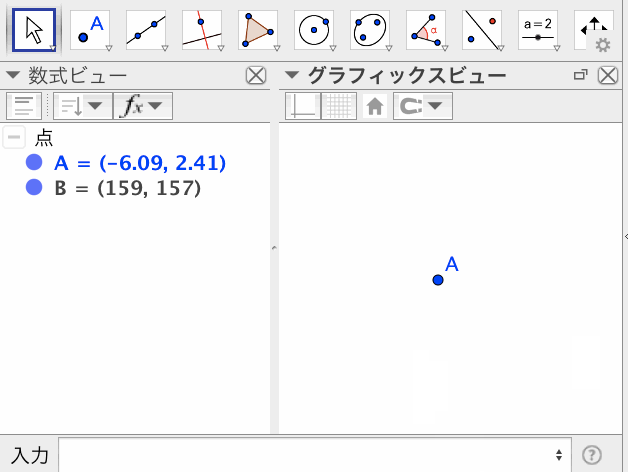
なお、PixelCoords[ InternalCorner[2] ]は、Corner[5]と同じ値(点)を返す。
ピクセル点:PixelPoint[ <数値w>, <数値h> ]
グラフィックスビューの左上隅から、右にwピクセル、下にhピクセルの位置にある点を返す。
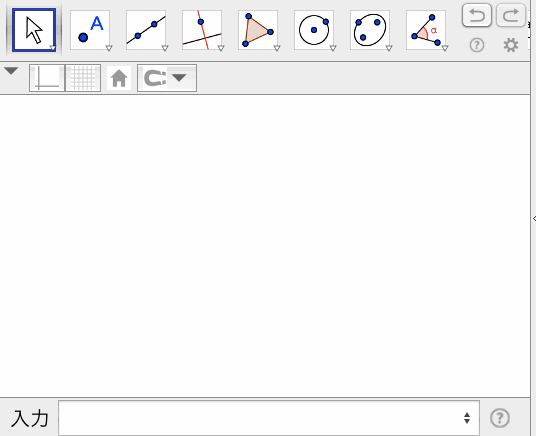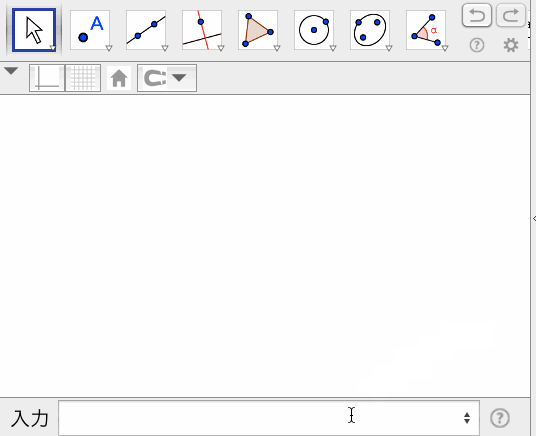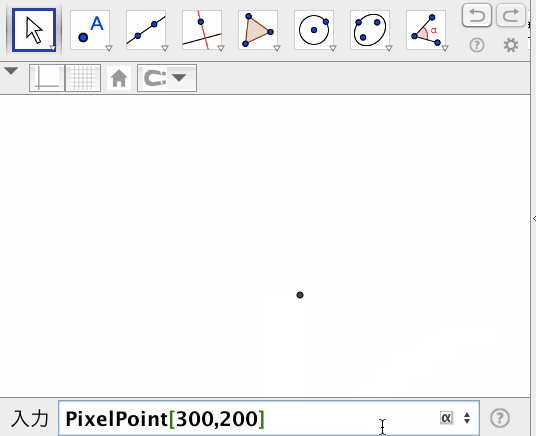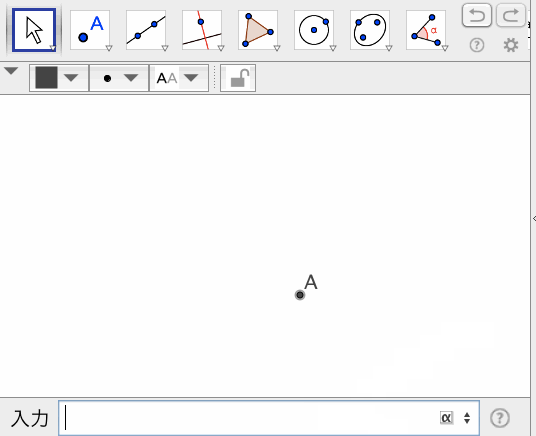
ピクセルグリッド:PixelGrid[ <数値> ]
グラフィックスビューの左上隅を始点として、指定したピクセル数(整数以外を入力した場合は、その数を越えない最大の整数)ごとに、グリッドを施す。
使用例としては、PixelGrid[10], PixelGrid[50], PixelGrid[100]を作成し、スタイルを適宜設定すれば、ピクセル数の目盛として利用できる。