GeoGebraで多角形の内部・辺上にある全ての格子点を返す方法
こんなことができます
下記のアプレットのように、多角形の内部・辺上にある格子点を表示させ、その数を計算できます。
下記のアプレットは、実際に頂点ABCをドラッグして、格子点の数がどう変化するかを確かめることができます。
準備
①任意の多角形を作成し、名前をusipolyとします。名前は、格子点を作成し終わるまでは変えないでください。
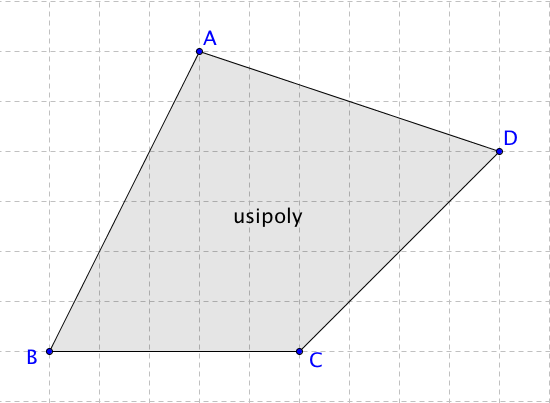
多角形の内部および辺上にある全ての格子点を返す方法
入力バーに、以下のコマンドをコピペします。
RemoveUndefined[Sequence[If[IsInRegion[Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], n], usipoly] ≟ true, Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], n], false], n, 1, Length[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]]]]]
すると、格子点がリストとして作られます。
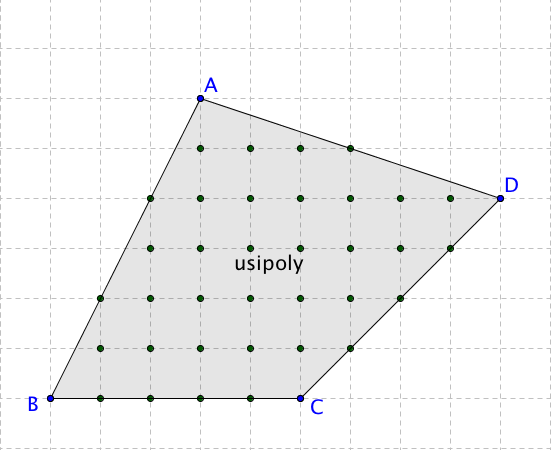
格子点を作成した後であれば、多角形の名前(usipoly)は自由に変更しても大丈夫です。
内部および辺上の格子点の数を数値オブジェクトとして返すには、以下のコマンドを入力バーにコピペします。
Length[RemoveUndefined[Sequence[If[IsInRegion[Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], n], usipoly] ≟ true, Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], n], false], n, 1, Length[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]]]]]]
多角形の辺上にある全ての格子点を返す方法
入力バーに、以下のコマンドをコピペします。
RemoveUndefined[Sequence[If[Distance[Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], m], PolyLine[Join[{{Vertex[usipoly]}, First[{Vertex[usipoly]}]}]]] ≟ 0, Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], m], false], m, 1, Length[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]]]]]
すると、格子点がリストとして作られます。
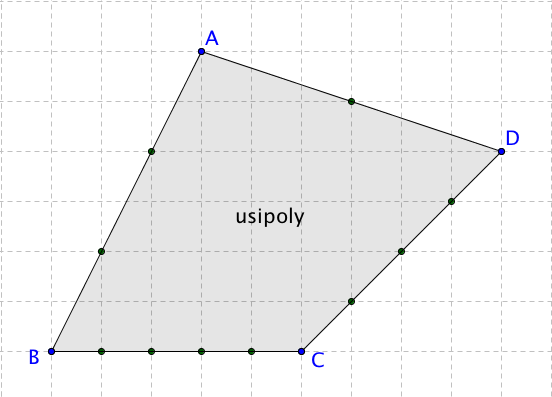
格子点を作成した後であれば、多角形の名前(usipoly)は自由に変更しても大丈夫です。
辺上の格子点の数を数値オブジェクトとして返すには、以下のコマンドを入力バーにコピペします。
Length[RemoveUndefined[Sequence[If[Distance[Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], m], PolyLine[Join[{{Vertex[usipoly]}, First[{Vertex[usipoly]}]}]]] ≟ 0, Element[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]], m], false], m, 1, Length[Flatten[Sequence[Sequence[(g, h), g, floor(Min[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[x(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1], h, floor(Min[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]), floor(Max[Sequence[y(Element[{Vertex[usipoly]}, i]), i, 1, Length[{Vertex[usipoly]}]]]) + 1]]]]]]